SDF Decomposition
September 7th, 2021
Abstract
Signed distance functions are a wonderful way to describe 3D shapes. They're simple to implement, they're a powerful way to make
programmatic art, and doing so can bring years of great fun into the life of the unsuspecting graphics programmer. While experimenting
with using tessellation as a means of rendering signed distance fields quickly, I came up with
a nice way to traverse signed distance functions for geometry
processing. This approach is generally useful for other rendering strategies, and this post is about how to use it for very fast
ray marching.
For ray marching, the strategy works like this:
-
Describe your model as a tree data structure where the leaves are simple distance functions, and the other nodes are either
CSG operators or transforms.
-
Traverse the tree from the root to the leaves. For a given leaf, calculate the shape's world space AABB and return it along with
the CSG subtree needed to render only that leaf.
-
Propagate these AABBs and associated subtrees from the leaves back to the root. As you descend the tree, apply transforms to the
AABBs. CSG operators typically split and discard AABBs. For example, the difference operator will return a set of AABBs for the
regions of the LHS operand not affected by the cut, and an AABB for the intersection between the LHS and RHS operands. The AABBs
returned by the difference operator (and others) will have a mix of subtrees for the passing operands and the combining region.
-
When you have returned to the graph root, you will have a set of AABBs with associated subtrees. Group these AABBs by subtree.
The set of unique subtrees provides the different shaders needed to render the image, and the AABB groups provide tight bounding
boxes for ray marching those shaders. If the root node is a union operator, then all of the subtrees will describe a simpler
shader than the original model.
-
Translate the subtrees to GLSL and compile the shaders.
-
Finally, to render the frame, draw each shader once per associated bounding box. Place the ray start position on the surface of
the bounding box, and discard if the ray leaves the bounding box. Depth testing must be enabled, and the draws should emit the
appropriate depth value for the ray hit.
Tangible!
Say we have this CSG tree:
'(union
(cube 3)
(diff
(cube 4)
(move -2 -2 2
(sphere 5))))

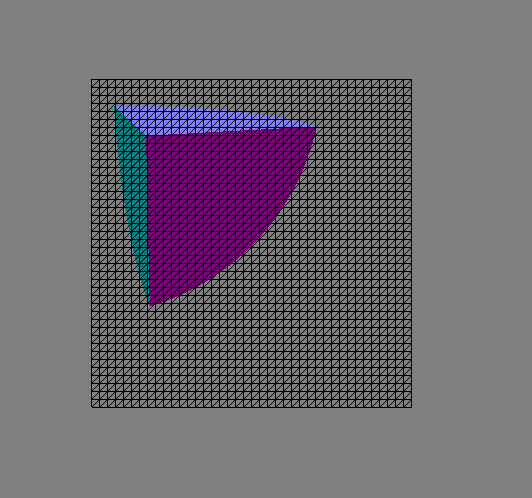
The traversal algorithm described above will break it down into these subtrees. The black lines in the pictures show the combined
tile coverage of the associated bounding boxes.
'(diff
(cube 4)
(move -2 -2 2
(sphere 5)))
; 1 bounding box.
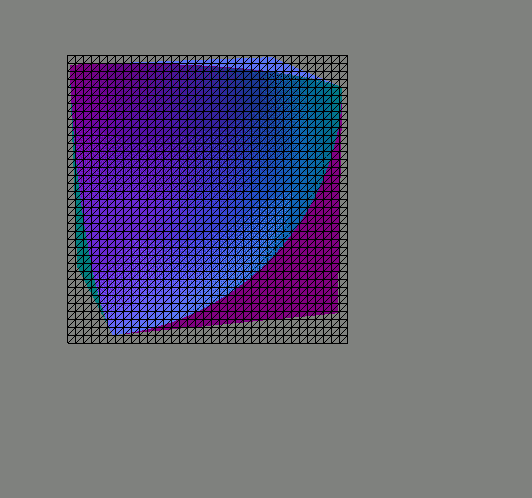
'(cube 4)
; 7 bounding boxes.

'(cube 3)
; 1 bounding box.
Why Does This Work?
Conventional ray marching typically evaluates the entire CSG tree at least once per step, regardless of if it is possible
to hit a given leaf in the tree.
On the other hand, the decomposition approach described above breaks the CSG tree down into simpler elements, and needs to
use a z-buffer to sort the results. As the ray marching area is tightly bound with this method, the iterations needed to
converge are lower on average. This approach is also a nice fit for cluster culling algorithms.
However, the real magic here is the depth buffer allows for the union operator to be a simple pass through for its operands.
Limitations
-
The CSG tree needs to be statically solvable. It's plausible that you could produce a variant where parameters don't
have known values at evaluation time, but it would probably require generating a significant number of subtrees, and
I'm not sure how the AABB splitting would work.
-
If your root node is an intersection operator, then only one variant will be produced.
Ideas
-
This approach fits nicely with cluster culling algorithms. Rather than a triangle strip, clusters are instead the bounding
boxes, and can be further constrained to screen space tiles.
-
In my experimentation so far, this approach produces a relatively low number of subtrees and the traversal algorithm is
reasonably fast. While the CSG tree needs to be statically solvable, it could be viable to perform occasional live changes
to the CSG tree on platforms where shaders can be compiled at runtime. This requires the ability to compile the shaders
without blocking rendering, and a fallback method for rendering CSG trees until their bounded versions are ready.
-
While the CSG tree needs to be statically solvable, the placement in the world can be dynamic. All that is needed is
an additional transformation at render time to move the ray into object space.
-
It might be worthwhile to further split expensive regions into smaller bounds for tighter culling.
-
Subtrees containing only simple shapes with well known ray hit tests could be traced much faster without ray marching.
Rasterizing geometric imposters might also be used to good effect.



